| |
Asynchronous Circuit and System Design Group | ||
Asynchronous Open-Source DLX Processor (ASPIDA)
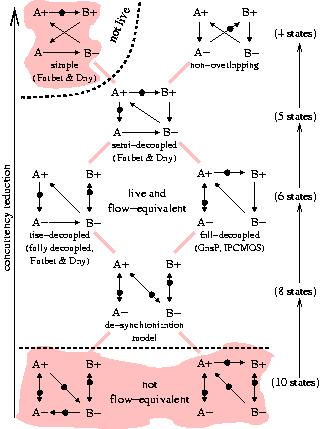 Provided the existence of the asynchronous controllers illustrated in the figure above, the designer of an asynchronous system must take the decision which one of these controllers is suitable for de-synchronization. Instead of studying them one by one, we present a simple study of four-phase protocols. The figure describes a partial order defined by the degree of concurrency of different protocols. Each protocol has been annotated with the number of states of the corresponding state graph. The marked graphs in the figure do not contain redundant arcs. An arc in the partial order indicates that one protocol can be obtained from the other by a local transformation (i.e. by moving the target of one of the arcs of the model). For example, the semi-decoupled protocol (5 states) can be obtained from the rise-decoupled protocol (6 states) by changing the arc A+  B- to the arc A+ B- to the arc A+  B+, thus reducing concurrency.
B+, thus reducing concurrency.The model with 8 states, labeled as ``de-synchronization model'', corresponds to the most concurrent model presented in "Handshake Protocols for De-synchronization" for which liveness and flow-equivalence is also proved in this paper. The other models are obtained by successive reductions or increases of concurrency. The nomenclature rise- and fall-decoupled has been introduced to designate the protocols in which the rising or falling edges of the pulses have been decoupled, respectively. The rise-decoupled protocol corresponds to the fully decoupled one proposed by Furber & Day in "Four-phase micropipeline latch control circuits" [4]. As it will be shown below, all models in the figure above, except those that are shadowed, are suitable for de-synchronization. For that, we will analyze the properties of liveness and flow-equivalence. We will focus on the liveness of the two sequential protocols: simple and non-overlapping. We will illustrate intuitively the liveness proofs of these protocols by trying to pass the acid test mentioned above: building a two-stage ring. It is clear that the non-overlapping protocol is live, given that this is the protocol to which the most concurrent model reduces when two controllers are connected back-to-back. However, the simple four-phase protocol does not pass this test: A+ ---> B+ ---> A- ---> B- ---> .... . Any trace will eventually visit a state in which A=B=1 which will produce data overwriting in the ring. To avoid data overwriting and deadlock, at least three latches in a ring are required, with only one data token circulating. That would require substituting each flip-flop with three latches, which would in turn introduce a potentially substantial penalty in terms of both area and performance. For the models with less than 8 states, obtained by concurrency reduction, the property of flow-equivalence holds automatically, since the traces produced by any of these models are always traces of the most concurrent model for de-synchronization, for which flow-equivalence has been proved in "Handshake Protocols for De-synchronization". On the other hand, the two models at the bottom, with 10 states each, have been obtained by increasing concurrency. The model on the left is obtained by changing the arc B- ---> A+ to the arc B- --->A-. This would correspond to shifting the arrow A+ <--- B- one step forward and converting it into A- <--- B-. It can easily be deduced that this transformation can produce data overwriting on latch B, since the value of A can change without having stored the previous value in B. Therefore, this model does not preserve flow-equivalence. The model on the right is obtained by changing the arc A+ ---> B- to the arc A+ ---> B+. It can be easily shown that this model does not preserve flow-equivalence either. Both models at the bottom of the figure are unsafe, since the arcs between events of the control signals for A and B can hold two tokens in some reachable markings. The conclusion is that all handshake protocols in the figure above, excepting the simple four-phase protocol and the two models at the bottom, are suitable for de-synchronization. Only the specific implementation characteristics of each one (area, power, performance) determine the best choice. |
|||