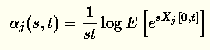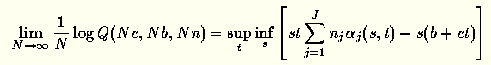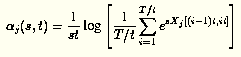Large Deviation Techniques for Traffic Engineering
Large Deviation Techniques for Traffic Engineering
This page contains some references, both theoretical and experimental
using real traffic,
on the application and evaluation of large deviation techniques,
and in particular the many sources asymptotic
and its related effective bandwidth definition, for traffic
engineering in broadband networks.
It also describes and makes available
the programs (executables) used
for obtaining the results published in [CSS99,
CSS98].
A description of the methods and usage of the tools is
available in [CS00b,CS99].
Also available is an interface providing Web-based access to the tools.[CS00]
E-mail suggestions
to vsiris "at" ics ``dot'' forth ``dot'' gr
Contents:
Motivation
Analysis of traffic measurements has shown that a
large variety of traffic types exhibit a
self-similar or fractal behavior. Such behavior can have implications
on the performance of a link that mulitplexes such traffic.
Hence, there is a need to understand the impact of the various
time scales of traffic burstiness on the performance of a link and on
its resource sharing capabilities.
Moreover, problems in
admission control,
network resource dimensioning, and pricing can be simplified
with the use of
an accurate and unifying definition of resource usage.
Some specific questions in traffic engineering that we seek
to answer are the following:
-
How is the loss probability (or probability of traffic exceeding
some maximum delay) affected by the traffic mix (percentage and
characteristics of the multiplexed traffic types)
and the link resources (capacity
and buffer)?
- For a link with some amount of
resources (capacity and buffer), what combinations of traffic sources can be
accepted, while still ensuring the target quality of service?
- What is the effect of traffic control
mechanisms, such as traffic shaping and priority scheduling,
on a link's multiplexing capability and the amount of resources
used by a bursty source?
- Measurement platforms enable the collection
of detailed packet level traces on high speed links.
Such traces can lead to a huge amount of data.
Can one collect a smaller amount of traffic statistics,
such as the amount of traffic in time periods of equal length,
that nevertheless contains all the necessary information for performance
analysis?
What is the sufficient time granularity (length of the measurement
period) of such measurements?
Traditional queueing theory based on elaborate traffic models
cannot answer such questions in the context of large multi-service
networks carrying traffic of different type.
Our objective is to address the above questions
and other problems in traffic engineering
by applying, to real broadband
traffic and a real
networking environment,
some powerful results from large deviations theory.
The theory
This work is based on the following definition of
effective bandwidths of
a source of type j
given by Kelly [Kel96]:
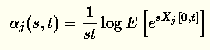
where Xj[0,t] is the amount of workload produced by a
source of type
j in a time interval of length t.
The above definition summarizes the statistical characteristics
of a source over different time and space scales.
When used for the analysis of a link (multiplexer) that guarantees some
level of performance or quality of service (QoS),
the space and time parameters s,
t characterize the context of the source,
which includes the link resources (capacity and buffer), scheduling
discipline, QoS, and
traffic mix (percentage and characteristics
of the different source types).
In this case, parameters s,
t can be computed using the many sources asymptotic
[CW96,BD95]:
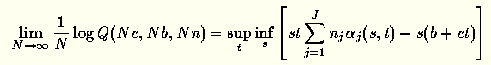
where Q(Nc,Nb,Nn) is probability of overflow in a
link with capacity Nc and buffer Nb
which multiplexes Nn=N(n1, ... nJ) sources, with
nj the percentage of sources of type j.
We will refer to the last equation as the supinf formula.
At this point you're probably asking why there is a need for an
effective bandwidth definition
which takes into account the context of the source.
Here's an answer.
and its application
Particular
values of (s,t) can be taken to characterize
the operating point of a link.
Here's why.
We have implemented the numerical solution of the
supinf when the source trace is in the form of
aggregate statistics (number of bytes/cells)
in fixed time intervals (epochs). A sample trace file looks like this
# epoch_in_msecs = 40
65
4
5
8
...
In the above trace an epoch has duration 40 msec.
In the first epoch ( 40 msec ) the source produces 65 cells,
in the second ( 40-80 msec ) 4 cells, etc.
To numerical solve the supinf formula
we replace the expectation in the effective bandwidth
with the empirical estimate. Hence the effective bandwidth
is estimated from traffic traces using the following equation:
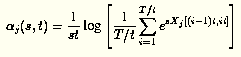
where T is the total duration of the trace (for simplicity we
have assumed that it is an integer number of the time parameter
t).
Xj[(i-1)t,it]
is the amount of work (e.g., number of cells)
produced in the interval ((i-1)t,it].
The supinf formula involves two
optimization procedures: the first consists of, for fixed
t, a minimization with respect to
s, and the
second a maximization with respect to t.
The minimization with respect to s
(infs) can be solved
numerically in an efficient manner by taking into account
the convexity of the product s times the effective
bandwidth, in s. In particular, for a specific value
of t, the infs is found
using a golden section search starting
from an initial uncertainty interval
which contains the minimum. The search procedure
decreases the uncertainty interval in successive steps,
and stops when the width of the
uncertainty interval is less than some small number.
The maximization with respect to t
(supt) is found by linear
searching a range of values for t,
in steps equal to the epoch of the trace file (there is no general property
that we can take advantage of to use a faster approach, as we
did for the infs).
The range of t that is searched is determined heuristically
and depends, among others, on the buffer size:
the extremizing value of t is larger for larger buffer sizes.
I have made available some typical values of s,t for
MPEG-1 video,
Internet WAN traffic, and
a traffic mix of MPEG-1 video
and voice traffic.
There is also a
FAQs for the s,t parameters
Software (executables)
The executables for the msa tool, along with other traffic
engineering related executables, are available here.
There exists a
man page, and
a collection of frequently encountered problems.
We have started developing a WEB-based interface for our traffic
analysis tools. A prelimenary version of the interface is available
here.
A sample trace file (MPEG-1 compressed
video of Star Wars) can be found here. The trace
contains 40000 epochs, with each epoch having duration 40 msec.
Note that the trace file MUST have the extension .tr
If you choose to download and use the software, I'ld appreciate if
you send me an email
at vsiris@ics.forth.gr, possibly with some of your results !
References
Theoretical backround
- [Kel96] F.P. Kelly.
``Notes on effective bandwidths''.
In Stochastic Networks: Theory and Applications (Editors F.P. Kelly, S. Zachary and I.B. Ziedins) Oxford University
Press, 1996. 141-168.
- [CW96]
C. Courcoubetis, R. Weber. ``Buffer Overflow Asymptotics for a Buffer Handling many Traffic Sources''. Journal of Applied Probability, vol. 33, 1996.
[.ps.gz]
- [CKW97]
C. Courcoubetis, F.P. Kelly, R. Weber.
``Measurement-based usage charges in communication networks ''.
Statistical Laboratory Research Report 1997-19, University of Cambridge.
To appear in Operations Research.
- [BD95] D.D. Botvich and N.G. Duffield.
``Large deviations, the shape of the loss curve, and economies of scale
in large multiplexers''.
Queueing Systems, 20:293-320, 1995.
- [LM98]
L. Likhanov and R.R. Mazumdar.
``Cell loss asymptotics for buffers fed with a large number of
independant stationary processes''. In Proc. of IEEE INFOCOM'98.
- [Wis99]
D. Wischik. ``The output of a switch, or, effective bandwidths
for networks''. To appear in Queueing Systems.
Application and experimental results
- [CS00b]
C. Courcoubetis and V.A. Siris.
``Procedures and tools for analysis of network traffic measurements''. Submitted,
September 2000.
- [CS00]
C. Courcoubetis and V.A. Siris.
``A web-based tool for advanced statistical analysis of network traffic measurements''.
July 2000.
[pdf, .ps.gz]
- [CS99]
C. Courcoubetis and V.A. Siris.
``Measurement and analysis of real network traffic''.
In Proc. of 7th Hellenic Conference on
Informatics (HCI'99), Ioannina, Greece, August 1999.
Available as ICS-FORTH TR-252
[pdf, .ps.gz]
- [CSS99]
C. Courcoubetis, V.A. Siris, and G.D. Stamoulis.
``Application of the Many Sources
Asymptotic and Effective Bandwidths to Traffic Engineering''.
Telecommunication Systems, 12(2-3):167--191, 1999.
[Abstract]
Preprint: [pdf, .ps.gz, html]
- [CDS99]
C. Courcoubetis, A. Dimakis, and G.D. Stamoulis.
`` Traffic Equivalence and Substitution in a Multiplexer''.
In Proc. of Infocom'99, New York, USA, March 1999.
[.ps.gz]
- [CSS98]
C. Courcoubetis, V.A. Siris, and G.D. Stamoulis. ``Application and Evaluation of Large Deviation Techniques for
Traffic Engineering in Broadband Networks''.
In Proc. of ACM SIGMETRICS '98/ PERFORMANCE '98, Madison,
Wisconsin, June 1998.
Superseded by [CSS99] above.
- [Gib96]
R. Gibbens. ``Traffic characterisation and effective bandwidths for broadband network traces''. Statistical Laboratory Research Report 1996-9, University of
Cambridge.
Related
ICS-FORTH Telecommunications and Networks Division
Email questions/problems to Vasilios A. Siris, vsiris "at" ics ``dot'' forth ``dot'' gr
Last updated: September 2000