First of all, they are the parameters that appear in the effective bandwidth definition of [Kel96]

When used for the analysis of a link (multiplexer) that guarantees some level of performance or quality of service (QoS), parameters s, called the space parameter, and t, called the time parameter, characterize the context of the source, which includes the link resources (capacity and buffer), scheduling discipline, QoS, and traffic mix (percentage and characteristics of the different source types).
Parameter s indicates the degree of statistical multiplexing: Large values of s indicate a low degree of statistical multiplexing; such is the case when we multiplex streams with peak rates not much smaller than the link capacity. On the other hand, small values of s indicate a large degree of statistical multiplexing; such is the case when we multiplex streams with peak rates much smaller than the link capacity. Furthermore, s=infinity corresponds to the case of deterministic multiplexing (i.e., zero probability of overflow). A more mathematical interpretation is the following: over the busy period preceding a buffer overflow the amount of work produced by a stream is exponentially tilted, with tilt parameter s.
 ,
where
,
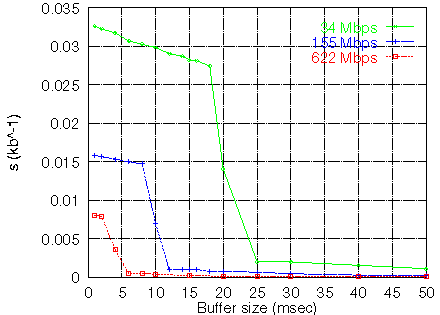
where 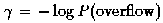 .
Hence, s
can be estimated using the ratio of differences
.
Hence, s
can be estimated using the ratio of differences
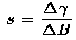 (e.g., see
(e.g., see
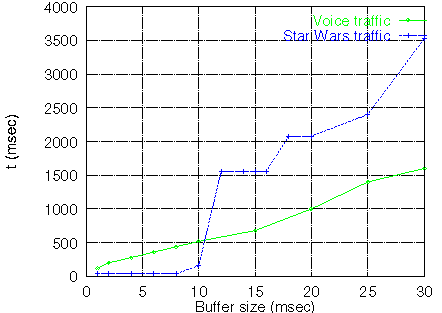
 Star Wars traffic
Star Wars traffic
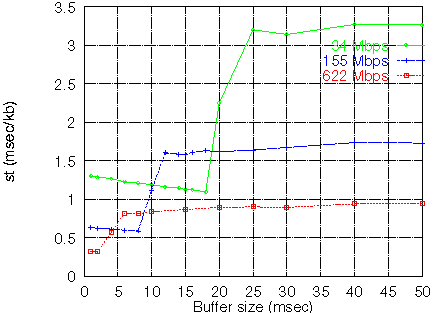
 C=155 Mbps
C=155 Mbps
 C=155 Mbps
C=155 Mbps
 Star Wars traffic
Star Wars traffic
 C=155 Mbps
C=155 Mbps
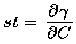 ,
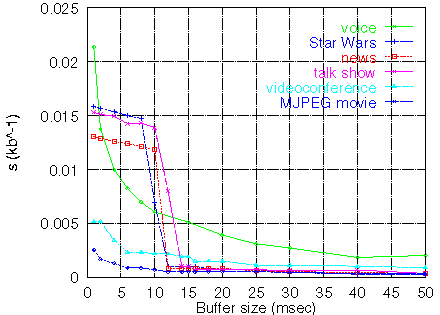
hence the product st indicates
how much the QoS increases when the capacity increases.
When there is a large degree of multiplexing st
obtains large values. This occurs because when there is a
large degree of multiplexing, t is large
hence the streams, for the overflow phenomena, appear smooth.
But for smooth traffic, the QoS is affected a lot by changes of the
capacity.
,
hence the product st indicates
how much the QoS increases when the capacity increases.
When there is a large degree of multiplexing st
obtains large values. This occurs because when there is a
large degree of multiplexing, t is large
hence the streams, for the overflow phenomena, appear smooth.
But for smooth traffic, the QoS is affected a lot by changes of the
capacity.
 Star Wars traffic
Star Wars traffic 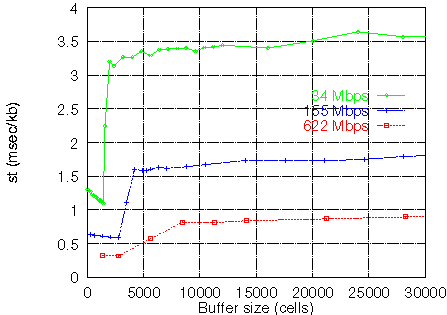 Star Wars traffic
Star Wars traffic