Asynchronous Circuit and System Design Group

Asynchronous Open-Source DLX Processor (ASPIDA)

General de-synchronization model

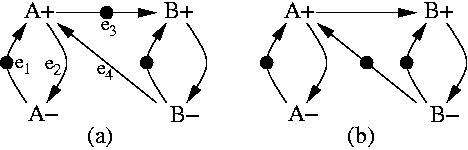
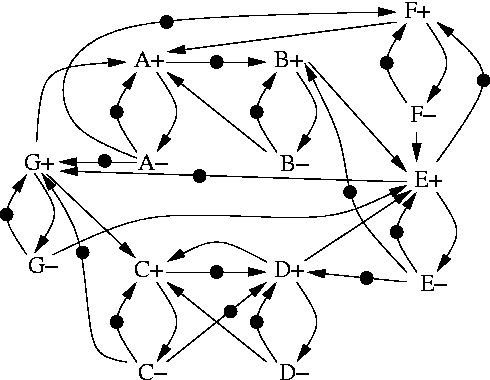
By taking as an example the overlapping model, we now show that it can be used for any arbitrary synchronous netlist, while preserving a property that makes the de-synchronized circuits observationally equivalent to their synchronous versions: flow equivalence [5].

The method for de-synchronizing an arbitrary netlist relies on composition of the controllers. We just identify pairwise interactions between adjacent latches, and then the overall clock generation circuit is obtained through composition of MGs corresponding to these partial descriptions. This procedure creates a marked graph of a certain class that we will call circuit marked graph (CMG).

The specification of a pairwise interaction between even-odd and odd-even latches for overlapping de-synchronization is shown in Figure 1. It models the communication of data from latch A to latch B. These patterns exactly correspond to the ones used in the behavioral specification of a linear pipeline. The only difference is that we added two auxiliary arcs A- to A+ and B- to B+ to model the behavior of the abstracted parts of the system (those that precede A and succeed B).

Figure 2 depicts the de-synchronization MG, as obtained by composition of patterns from Figure 1.

**Figure 1:** Synchronization between latches: (a) even to odd, (b) odd to even.
$\begin{figure}\centerline{\psfig{figure=Fig/pair.eps,width=0.6\linewidth}}\vspace*{-4.5mm} \end{figure}$

**Figure 2:** Model for the circuit in Fig 1.
$\begin{figure}\centerline{\psfig{figure=Fig/stgnet.eps,width=0.4\linewidth}}\vspace*{-4.5mm} \end{figure}$

Properties of the general model

We now discuss several properties of the model. The proofs of the theorems are presented in [3].

Theorem 3.2 Any circuit marked graph is live and safe.

Safeness guarantees that no data overwriting will occur. Liveness guarantees something crucial for the model: absence of deadlocks. At this point, it is important to emphasize that the controller for de-synchronized clocks presented in this document has self-resetting pulses, i.e. the only causality arc that precedes an event X- is the corresponding X+. This spontaneous ``return-to-zero'' guarantees liveness for any netlist, even cyclic ones.