Asynchronous Circuit and System Design Group

Asynchronous Open-Source DLX Processor (ASPIDA)

Timed model

Computational blocks and latches have delays that impose a set of timing constraints for the model to be valid.

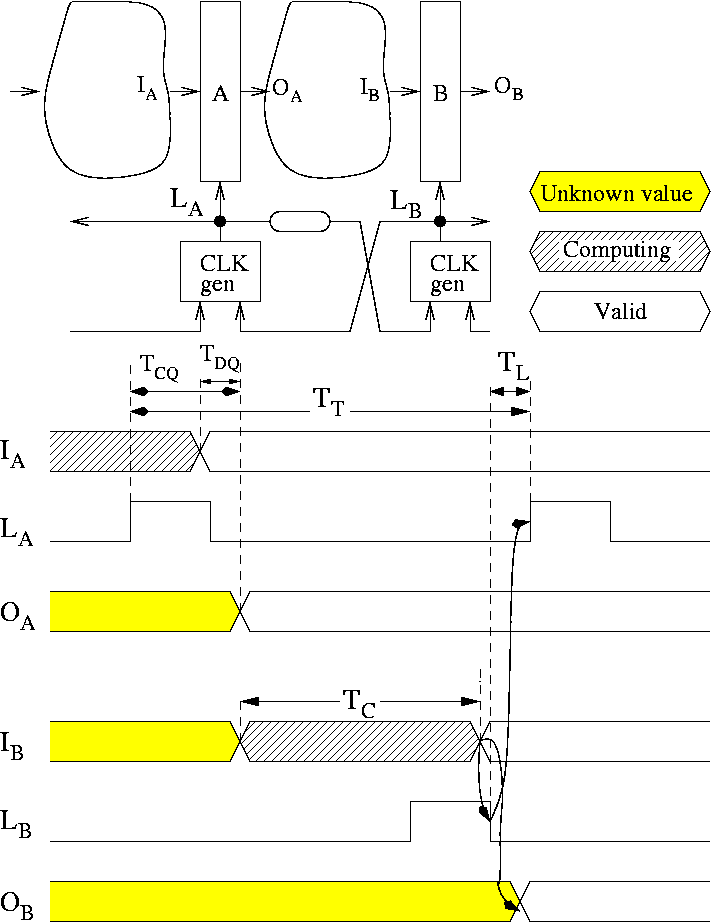
Figure 1 depicts the timing diagram for the behavior of two latches in a pipeline. The signals I and O represent the inputs and outputs of the latches. The signal L is the control of the latch (L=1 for transparent).

We will focus our attention on latch A. As soon as OA becomes valid, the computation for block B starts. Latch B can become transparent before the computation completes. Opening a latch in advance is beneficial for performance, because it eliminates the time for capturing data from the critical path.

Once the computation is over, the local clock LB of the destination latch B immediately falls. This is possible because modern latches have zero setup time [1].

**Figure 1:** Timing constraints for the asynchronous controllers.
$\begin{figure}\centerline{\psfig{figure=Fig/timing_new3.eps,width=0.6\linewidth}}\vspace*{-4.5mm} \end{figure}$

Assuming that all controllers have similar delays the following constraint is required for correct operation.

TT >= TCQ + TC + TL

(1)

The constraint (1) indicates that the cycle time of a local clock (measured as a delay TT between two rising edges of LA), must be greater than the delay of local clock propagation though a latch (TCQ) plus the delay of the computational block (TC) plus the latch controller delay (TL). The control overhead in this scheme is reduced to a single delay TL because control handshake overlaps with the computation cycle due to the early rising of the local clock. The constraint assumes that the depth of combinational logic is sufficiently large to amortize the overlapping part of the handshake. The latter is true for ASIC designs, that often have more than 20 levels of logic between adjacent registers. However, we also tried examples, such as a DES encryption engine, which are extremely shallow, with similar results.

Inequality (1) guarantees the satisfaction of set-up constraints for the latch. Note that hold constraints in a de-synchronized circuit are ensured automatically, because the clock of any predecessor latch rises only after the clock of its successor latch had fallen. This makes it impossible to have races between two consecutive data items at latch inputs.

Timing compatibility

To prove that the suggested design methodology is modular and compositional we need to show that a de-synchronized circuit can replace its synchronous counterpart without disturbing the rest of a system (presumably synchronous). This can be achieved by comparing cycle times of de-synchronized and synchronous designs.

In a synchronous flip-flop-based circuit, the cycle time TS is bounded by [1]:

TS >= TC + Tsetup + Tskew + TCQ

(2)

where TC, Tsetup, Tskew and TCQ are maximum combinational logic, setup, skew and clock-to-output times respectively. Let us compare inequalities (1) and (2), bearing in mind that due to retiming the maximal computation time in a de-synchronized circuit can only be reduced. We can conclude that under reasonable timing assumption ( Tsetup + Tskew >= TL) the cycle time of de-synchronized circuit TT should not be larger than the cycle time TS of the corresponding synchronous design.

There is a small caveat in the above statement. The notion of a cycle time is well defined only for a circuit with a periodic clock. In a de-synchronized system the separation time between adjacent rising edges of the same local clock might change during functioning. Therefore when talking about de-synchronized and synchronous systems one has to relate the perfect periodic behavior of one of them to a non-periodic one of another.

Two facts proven in [3] help in establishing this relationship.

Latches that belong to critical computational paths of a de-synchronized system have a well-defined constant cycle time TT.
The rest of the latches might have variable cycle times in the finite prefix of a system functioning but finally must settle to constant cycle time TT.

This shows that the behavior of a de-synchronized circuit has a well-defined periodicity, similar to that of a synchronous one, paced by a common clock.

A de-synchronized circuit with cycle time TT can be embedded into a synchronous environment with a clock cycle TS by driving the latch controllers on its boundaries with the clock (as if it was coming from ``external'' controllers). This does not cause any meta-stability problems and satisfies setup and hold constraints, as long as TS >= TT. Under these conditions, boundary latches become critical, since they are paced by external clock TS. This makes de-synchronized and synchronous systems compatible in terms of timing, because their external timed behavior is the same.

One advantage of de-synchronization is that it eases some form of circuit binning based on performance. If we assume that the performance of similar objects (e.g. transistors, interconnects on the same layer) track each other within relatively small regions of the layout, we can assume that the performance of a die will be determined by the delay chains, while the delay of the logic will be proportionately smaller, and thus setup constraints will be automatically satisfied.

This means that the request and acknowledge wires at the boundaries of the circuit can be used to measure the worst-case response time of every individual die. In other terms, the maximum speed of a die can be established by only looking at the timing of transitions of some output signals with respect to the clock input, without the need for expensive at-speed delay testing equipment. This allows one to classify dies according to their maximum operational speed (binning), which so far was only used for leading-edge CPUs (from Intel, AMD, Sun) due to the huge cost of at-speed testing equipment. It also allows one to tune the process, by observing the performance of whole circuits, not just of small delay chains on test chips.