Asynchronous Circuit and System Design Group

Asynchronous Open-Source DLX Processor (ASPIDA)

Marked Graph Representation of De-synchronization model for a linear pipeline and a ring

This page presents a formal model for de-synchronization. The aim is to produce a set of distributed controllers that communicate locally with their neighbors and generate the control signals for the latches in such a way that the behavior of the system is preserved. For simplicity, we assume that all combinational blocks and latches have zero delay. Thus, the only important thing about the model is the sequence of events of the latch control signals.

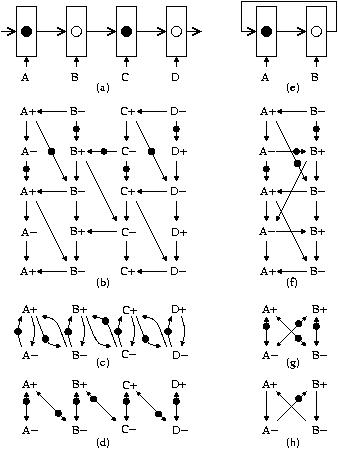
Figure 1

For simplicity we will start by analyzing the behavior of a linear pipeline (see Fig. 1(a)). Black dots represent data tokens, whereas white dots represent bubbles. In the model, we assume that all latches become transparent when the control signal is high. The events A+ and A- represent rising and falling transitions of the control signal A, respectively. Figure 1(b) depicts a fragment of the unfolded marked graph representing the behavior of the latches. There are three types of arcs in this model (we only refer to those in the first stage of the pipeline):

A+ --> A- --> A+, that simply denote that the rising and falling transitions of each signal must alternate.
B- --> A+, that denotes the fact that for latch A to read a new data token, B must have completed the reading of the previous token coming from A. If this arc is not present, data overwriting can occur, or in other terms hold constraints can be violated.
A+ --> B-, that denotes the fact that for latch B to complete the reading of a data token coming from A it must first wait for the data token to be stored in A. If this arc is not present, B can ``read a bubble'' and a data token can be lost, or in other terms setup constraints can be violated.

The marking in Fig. 1(b) represents a state in which all latch control signals are low and the events B+ and D+ are enabled, i.e. the latches B and D are ready to read the data tokens from A and C, respectively. Figure 1(c) shows the marked graph that derives from the unfolded graph in Fig. 1(b). A simplified notation is used in Fig 1(d) to represent the same graph, substituting each cycle x none

y by a double arc x none

y, where the token is located close to the enabled event in the cycle (y in the example).

It is interesting to notice that the previous model is more aggressive than the classical one generating non-overlapping phases for latch-based designs. As an example, the following sequence can be fired in the model of Fig (a-d):

D+ D- C+ B+ B- A+ C- .

After the events D+ D- C+ B+ , a state in which B=C=1 and A=D=0 is reached, where the data token stored in A is rippling through the latches B and C. A timing diagram illustrating this sequence is shown in Fig. 2

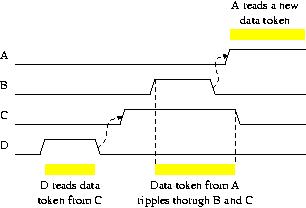
Timing diagram of the linear pipeline in Fig1(a-d)

Figure 2